DeltaConv：用于点云几何深度学习的各向异性算子

DeltaConv： 用于点云几何深度学习的各向异性算子

RUBEN WIERSMA, AHMAD NASIKUN等

GitHub：deltaconv

翻译自：(Wiersma et al., 2022)

摘要

受图像深度学习的成功和三维数据可用性增加的推动，从三维点云数据中学习的势头迅猛发展。在本文中，我们的目标是构建各向异性卷积层，直接作用于由点云导出的曲面。由于缺乏用于表面切向方向的全局坐标系，这具有挑战性。我们介绍的 DeltaConv 是一种卷积层，它结合了向量微积分中的几何算子，能够在点云上构建各向异性滤波器。由于这些算子是在标量场和矢量场上定义的，因此我们将网络分为标量流和矢量流，并通过算子将它们连接起来。矢量流使网络能够明确表示、评估和处理方向信息。我们的卷积既稳健又易于实现，在多个基准测试中与最先进的方法不相上下，甚至更胜一筹，同时还能加快训练和推理速度。

引言

卷积神经网络（CNN）在图像上的成功以及点云数据可用性的不断提高，促使人们将 CNN 从图像推广到三维点云[Bronstein 等人，2017 年；Guo 等人，2020 年；Liu 等人，2019d]。实现这一目标的方法之一是设计直接在曲面上运行的卷积。这种内在卷积将内核空间缩小为切线空间，而切线空间在曲面上是二维的。与外在卷积相比，内在卷积的效率更高，核的搜索空间也更小，它们自然会忽略空的空间，而且对刚性和非刚性变形都很稳健[Boscaini 等人，2016]。点云本征卷积的例子有 GCN [Kipfand Welling 2017]、PointNet++ [Qi 等人 2017b]、EdgeConv [Wang 等人 2019] 和 DiffusionNet [Sharp 等人 2021]。

我们的重点是构建各向异性或与方向相关的本征卷积。由于非线性流形缺乏全局坐标系这一基本挑战，这一点很难做到。为了说明这个问题，请看图像上的 CNN（图 1，左）。由于图像具有全局一致的向上方向，因此网络可以建立各向异性过滤器，以相同的方式激活整个图像。例如，一个滤波器可以检测垂直边缘，另一个可以检测水平边缘。无论图像中的边缘在哪里，滤波器的响应都是一致的。在后续层中，可以将这些滤波器的输出进行组合，例如，找到一个角落。由于我们在曲面上没有全局坐标系（图 1，右），因此无法像在图像上那样建立和使用各向异性滤波器。这就限制了目前对点云的固有卷积。例如，GCNs 滤波器是各向同性的。PointNet++ 使用最大聚合并添加相对点位置，但仍对每个相邻点应用相同的权重矩阵。

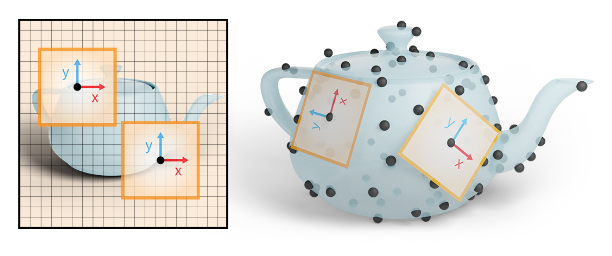
我们介绍了一种为几何 CNN 构建各向异性卷积层的新方法。我们的卷积是用几何算子而不是核来描述的。基于算子的视角是 GCN 所熟悉的，GCN 使用图上的拉普拉斯。虽然 Laplacian 非常适合曲面的内在学习，但它是各向同性的。创建各向异性算子的经典方法是将拉普拉斯函数写成梯度发散，并对中间向量场进行线性或非线性运算 [Weickert 1998]。在此基础上，我们从基本几何算子中构建了可学习的各向异性算子：梯度、共梯度、发散、卷积、拉普拉斯和霍奇拉普拉斯。这些算子定义在标量场和切线向量场的空间上。因此，我们的网络分为两个流：一个流包含标量，另一个包含切向矢量。算子沿着这两个流进行映射，并在这两个流之间进行映射。向量流编码沿表面的特征激活和方向，使网络能够在后续层中测试和关联方向。根据任务的不同，网络会输出标量或向量。由这些算子构建的网络具有与坐标无关的特性：虽然需要选择点云切线空间的基点，但无论选择什么基点，网络学习到的权重都是相同的。因此，尽管表面上缺乏全局坐标系，我们也可以实现与方向相关的卷积，而无需专门构建切空间基。我们将我们的卷积命名为 DeltaConv。

要了解 DeltaConv 的优势，可以考虑 Perona 和 Malik [1990] 提出的各向异性图像滤波器。Perona-Malik 滤波器整合了各向异性扩散方程，其中各向异性算子结合了梯度、非线性和发散。DeltaConv 可以访问构建这种各向异性算子所需的构件，并执行扩散方程的显式积分步骤。图 2 举例说明了这一点。我们训练了一个简单的 ResNet [He 等人，2016 年]，以匹配样本图像上二十个各向异性扩散步骤的结果。DeltaConv 可以很好地再现滤波器，而其他固有卷积和常规图像卷积则无法捕捉到这种效果，反而会产生过于平滑的信号或伪影。我们的方法还有以下优点：通过在整个网络中保持矢量特征流，我们的卷积可以将表面不同点之间的方向信息联系起来。正如我们在实验中展示的那样，由于各向异性，卷积的表现力得到了增强，因此与各向同性卷积以及最先进的方法相比，我们的准确性也得到了提高。此外，每个算子都以稀疏矩阵的形式实现，算子的组合按点计算，简单高效。

在我们的实验中，我们证明了仅有几个 DeltaConv 块的简单架构可以与使用更复杂架构的先进结果相媲美，在某些情况下甚至超过了先进结果。我们在 ModelNet40 上取得了 93.8% 的准确率，在 ScanObjectNN 最难的变体上取得了 84.7% 的准确率，在 ShapeNet 上取得了 86.9 mIoU 的准确率，在非刚性变形形状数据集 SHREC11 上取得了 99.6% 的准确率。我们的消融研究表明，与基于边缘的特征相比，添加矢量流可将 ModelNet40 的误差降低 25%（从 90.4% 降至 92.8%），将 ShapeNet 的误差降低 21%（从 81.1 mIoU 降至 85.1 mIoU），而使用每点方向特征可将推理速度提高 1.5 - 2 倍，将后向传递速度提高 2.5 - 30 倍。总结一下我们的主要贡献：

• 我们为几何 CNN 引入了一种新的卷积层结构，它支持各向异性滤波器的构建。这是通过让网络学习卷积作为几何微分算子和随点非线性的合成和线性组合来实现的。此外，除了通常的标量特征流之外，网络还能保持矢量特征流，并使用算子在流内和流之间进行通信。
• 我们提出了一种网络架构来实现我们的方法，并调整差分算子，使其在我们的网络中有效工作。
• 我们实施并评估了点云网络，并提出了应对点云学习中普遍存在的采样不足区域、噪声和信息缺失的技术。

相关工作

我们将对相关工作的讨论集中在最相关的主题上。请参考有关几何深度学习[Bronstein 等人，2021 年，2017 年]和点云学习[Guo 等人，2020 年；Liu 等人，2019d]的调查报告，以了解这一不断扩展的领域的更全面概述。

点云网络和各向异性

点云数据学习的常见方法是使用多层感知器（MLP）学习每个点的特征，然后进行局部或全局聚合。许多方法也会在最大聚合之前学习局部点对的特征。著名的例子有 PointNet 及其后继者 PointNet++ [Qi 等人，2017a,b]。一些后续研究通过增加更多的点对特征组合等方法提高了速度和精度[Le 等人，2020 年；Liu 等人，2020 年；Lu 等人，2021 年；Qiu 等人，2021a；Sun 等人，2019 年；Xu 等人，2021b；Yang 等人，2019 年；Zhao 等人，2019 年]。其中一些点向 MLP 通过拆分每个三维轴的 MLP 来明确编码各向异性[Lan 等人，2019 年；Liu 等人，2020 年]。来自变压器的概念 [Vaswani 等人，2017 年] 也已进入点云领域 [Lin 等人，2020 年；Zhang 等人，2021 年；Zhao 等人，2021 年]。这些网络使用自我关注来计算（相邻）点的聚合权重。通过添加三维空间的相对位置，将空间信息纳入其中。在我们的方法中，基于注意力的聚合可以用来替代最大聚合。点与点之间的距离可以作为内在的空间编码。

伪网格卷积是将图像卷积更直接地转换成点云

其中许多是在三维空间中定义的，因此支持三维坐标中的各向异性。有几项研究学习了连续核，并将其应用于局部点云区域[Atzmon等人，2018；Boulch，2020；Fey等人，2018；Hermosilla等人，2018；Liu等人，2019a,b；Thomas等人，2019；Wu等人，2019；Xu等人，2021a]。还有一些人学习离散核，并将局部区域的点映射到离散网格中 [Choy 等人，2019 年；Graham 等人，2018 年；Hua 等人，2018 年；Lei 等人，2019 年；Li 等人，2018 年]。我们通过建立本征卷积，进入了一个正交方向，本征卷积在更少的维度上运行，并自然地泛化为（非）刚性变形形状。

最后，基于图的方法从输入集创建 k 近邻图或半径图，并应用图卷积 [Chen 等人，2020 年；Dominguez 等人，2018 年；Feng 等人，2019 年；Liu 等人，2019 年 c；Pan 等人，2018 年；Shen 等人，2018 年；Simonovsky 和 Komodakis，2017 年；Te 等人，2018 年；Wang 等人，2018 年、2019 年；Zhang 等人，2019 年；Zhang 和 Rabbat，2018 年]。DGCNN [Wang 等人，2019] 引入了 EdgeConv 算子和动态图组件，可以重新连接网络内部的 k 近邻图。EdgeConv 计算特征差异的最大值，这使得网络可以在其通道中表示方向。如果将空间坐标作为输入，通道方向就会类似于空间方向，而 DGCNN 仅在第一层才会出现这种情况。相比之下，我们的卷积算法直接在算子中支持各向异性。

旋转等变方法

在点云和网格的旋转等变方法中，也使用了具有双流和矢量值特征的架构。一组作品研究了三维空间中的旋转等变，旨在设计不受刚性点云变换影响的网络[Cohen 等人，2018 年；Esteves 等人，2017 年；Poulenard 等人，2019 年；Thomas 等人，2018 年]。这一概念也被纳入变压器设置中[Fuchs 等人，2020]。旋变核通常输出向量值特征。矢量神经元通过线性组合三维矢量，再加上矢量非线性，简化了矢量神经元的使用[Deng 等人[n.d.]]。我们对向量 MLP 的使用与此类似。不同之处在于，我们使用的是切向矢量，而不是三维矢量，而且我们在网络内部使用几何运算符推导这些矢量。

另一种方法是利用网格上的固有旋转量变卷积建立网络[Cohen 等人，2019 年；de Haan 等人，2021 年；Gerken 等人，2021 年；Poulenard 和 Ovsjanikov，2018 年；Weiler 等人，2021 年；Wiersma 等人，2020 年]。这些网络使用局部参数化，并在参数域中应用旋转或轨则变量核，以实现与切线空间中基数选择的独立性。我们的方法是轨则参数网络的替代方案。微分算子的使用也使我们的网络不受局部坐标系选择的影响。我们这种方法的一个好处是不需要局部参数化。举例来说，轨则参数方法通常使用指数图进行局部参数化，但忽略了参数化引起的角度变形。据我们所知，我们是第一个在点云上实现和评估内在双流架构的人。

几何算子

多位作者使用几何算子构建卷积。图-拉普拉斯算子用于 GCN [Kipf and Welling 2017]。用于图形学习的光谱网络基于图-拉普拉奇的特征对[Bruna 等人，2014 年]。用于三角形网格的曲面网络 [Kostrikov 等人，2018] 将拉普拉斯与外在狄拉克算子交错在一起 [Liu 等人，2017]。Parametrized Differential Operators (PDOs) [Jiang 等人，2019] 使用梯度和发散算子来学习非结构网格上的球形信号。DiffGCN [Eliasof and Treister 2020] 使用梯度和发散算子的有限差分方案来构建图网络。DiffusionNet [Sharp 等人，2021 年] 使用拉普拉斯-贝尔特拉米算子和梯度方向特征学习扩散。DeltaConv 使用更多的算子集，将向量微积分中的算子进行组合和串联。此外，它还允许处理向量值特征流中的方向信息。一种相关的方法是 HodgeNet [Smirnov and Solomon 2021]，它可以学习使用微分算子的结构来构建算子。在深度学习之外，微分算子被广泛应用于三维形状分析 [Crane 等人，2013a；de Goes 等人，2016]。

方法

我们通过学习几何微分算子的组合来构建各向异性卷积。由于这些算子定义在标量场和矢量场上，因此我们将网络分为标量特征和矢量特征。在本节中，我们将介绍这两种流、算子及其离散化方式，以及算子组合的学习方式。最后，我们将讨论这一结构所产生的特性。

流，考虑一个点云 \(P \in \mathbb{R}^{N \times 3}\)，它由 \(N\) 个点组成的一个 \(N \times 3\) 矩阵排列而成。所有点都可以与 \(C\) 个额外特征相关联，这些特征存储在一个矩阵 \(X \in \mathbb{R}^{N \times C}\) 中。在网络内部，我们将第 \(l\) 层在第 \(i\) 个点的特征称为 \(x_i^{(l)} \in \mathbb{R}^{C_l}\)。所有这些特征构成了标量流（scalar stream）。

矢量流（vector stream）与标量流并行运行。矢量流中的每个特征是一个切向量，通过系数 \((\alpha_i^u, \alpha_i^v)\) 编码，这些系数相对于相应切平面中的基。基可以是任意一对与法向量正交的标准正交向量。系数对每个点交错排列，形成特征矩阵 \(V^{(l)} \in \mathbb{R}^{2N \times C_l}\)，其中 \(V^{(l)}\) 的一列是系数：\([\alpha_1^u, \alpha_1^v, \ldots, \alpha_i^u, \alpha_i^v, \ldots, \alpha_N^u, \alpha_N^v]^T\)。矢量流的输入是在每个点定义的矢量场。在我们的实验中，我们使用输入到标量流的梯度作为矢量流的输入。我们将分别称 \(X\) 和 \(V\) 的连续对应物为 \(X\) 和 \(V\)。

在点云上，每一个点都可以具备各种属性或特征，这些特征可以是标量的，也可以是矢量的

比如，一辆汽车表面离散化出来的点云模型，每个点上都可以有：1. 标量特征，温度、颜色、湿度；2. 矢量特征，风速等等

标量到标量：最大聚合

在标量流内部应用了一个简化版的基于点的 MLP（多层感知机），基于 PointNet++ [Qi et al. 2017b] 和 EdgeConv [Wang et al. 2019]。我们对每个点应用一个 MLP 然后对一个 \(k\)-最近邻居 \(\mathcal{N}(i)\) 执行最大值聚合。标量流中的特征被计算为

\[x_i^{(l+1)} = h_{\theta_0}\left(x_i^{(l)}\right) + \max_{j \in \mathcal{N}(i)} h_{\theta_1}\left(x_j^{(l)}\right)\]

其中 \(h_{\theta_0}\) 和 \(h_{\theta_1}\) 表示多层感知机（MLP），由全连接层、批量归一化 [Ioffe and Szegedy 2015] 和非线性函数组成。如果点位置被用作输入，它们会在最大聚合之前中心化：\(\hat{p}_j = p_j - p_i\)。

与 EdgeConv 和 PointNet++ 最大的不同是，我们在网络中只使用基于点的特征，而不是基于边的特征。因此，MLP 内部使用的矩阵乘法不是应用于\(kN\)个特征向量，而是应用于\(N\)个点特征向量。这对前向和后向传递的运行时间有很大影响。方向信息是用每点向量而不是边来编码的。

这个过程主要在于：1. MLP混合标量特征组成的向量， 2. 提取K近邻中最大值做局部特征捕捉

这里特别强调：1. 如果使用的是位置信息，要相对距离化，2. 不使用基于边的特征，即不侧重于点与点之间的关系和相互作用

标量到矢量：梯度与余梯度

梯度和余梯度算子连接标量流到矢量流。一个函数的梯度代表了在每个点最大的变化率及其变化方向的向量。余梯度是梯度的 90 度旋转。结合起来，梯度和余梯度跨越了切平面，允许网络对梯度向量进行缩放、倾斜和旋转。

我们使用一个移动最小二乘法构建了一个离散的梯度算子，该方法在具有 \(k\) 邻居的邻域上使用 [Nealen 2004]。这种方法用于对点云进行建模和处理，以及在点云上解微分方程 [Crane et al. 2013b; Liang 和 Zhao 2013]。该过程和伴随理论概述在补充材料中。梯度算子被表示为一个稀疏矩阵 \(G \in \mathbb{R}^{2N \times N}\)。它接受 \(N\) 个值代表点上的特征，并输出 \(2N\) 个值代表每个点的切线基系数中的梯度。矩阵非常稀疏，因为它每行只包含 \(2k\) 个元素。余梯度算子 \(JG\) 是梯度与一个块对角稀疏矩阵 \(J \in \mathbb{R}^{2N \times 2N}\) 的组合，其中 \(J\) 的每个块是一个 \(2 \times 2\) 的 90 度旋转矩阵。

点云通常包含欠采样区域和噪声。这对移动最小二乘法过程可能是个问题。考虑图 3 中的一个例子，一把腿细的椅子。只有少数点沿着构成椅子腿的线排列。因此，垂直于线的方向是欠采样的，导致在一个不稳定的最小二乘拟合中：一点的微小扰动可能严重影响结果（左侧，圈出区域）。我们通过添加一个由 \(\lambda\) 缩放的正则化项到最小二乘拟合过程中，试图减轻这种效应（右侧）。这是一个被称为岭回归或Tikhonov正则化的已知技术。

我们还主张梯度算子应该被规范化，这一观点是由信息在网络中如何融合激发的。如果 \(G\) 表现出发散或收敛行为，由 \(G\) 产生的特征也将发散或收敛。当梯度在网络中被多次应用时，这是不可取的。由梯度操作产生的特征将具有不同的数量级，网络权重需要考虑这一点。因此，我们通过 \(\ell^{\infty}\) 算子范数规范化 \(G\)，提供了一个操作子缩放行为的上界

\[\hat{G} = \frac{G}{\|G\|_{\infty}}, \quad \text{其中} \|G\|_{\infty} = \max_i \sum_j \|G_{ij}\|\]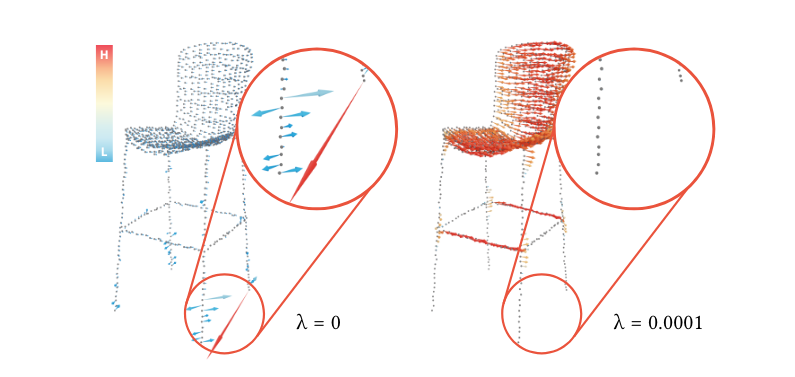

矢量到标量：散度、旋度和范数

矢量流通过散度、旋度和范数连接回标量流。这些算子通常用来分析矢量场，并指示诸如汇点、源点、旋涡以及矢量场的强度等特征。网络可以使用它们作为各向异性算子的构建块。 离散散度也是用移动最小二乘法构建的，该方法在补充材料中有描述。散度表示为一个稀疏矩阵 \(D \in \mathbb{R}^{N \times 2N}\)，有 \(2kN\) 个元素。旋度被导出为 \(-DJ\)。

矢量到矢量：Hodge Laplacian

矢量特征在矢量流中通过身份矩阵 \(I\) 和 Hodge Laplacian \(\Delta\) 的组合进行扩散。将 Hodge Laplacian 应用于矢量场 \(V\) 会得到另一个矢量场，它编码了每个点及其邻居的矢量之间的差异。Hodge Laplacian 可以被构造为梯度（grad）、散度（div）、旋度（curl）和 \(\mathcal{J}\) 的组合 [Brandt et al. 2017]。

\[\Delta = -(\text{grad div} + \mathcal{J} \text{ grad curl})\]

在离散设置中，我们用其离散变体替换每个算子，

\[L = -(GD - JGDJ)\]

为什么选择这些算子？

我们使用的算子在本质上是相互关联的。它们构成了表面 de Rham 复合体的一个度量版本 [Wardetzky 2006]。以下图表阐述了前面章节中描述的连接，每个算子都在函数（标量场）和矢量场之间进行映射。

请注意，底行是顶行的一个 90 度旋转版本。如果我们按照从左到右的图表应用 grad 然后是 curl 到任何函数，输出将总是零。从右到左的路径也是如此。列出的算子是一阶导数。拉普拉斯算子，作为二阶导数，可以通过组合一阶算子形成。对于函数：用 grad 和 div 再次返回矢量场（Laplace-Beltrami）。对于矢量场：我们用 div 和 curl 去到标量，然后再用 grad 和 co-grad 返回（Hodge-Laplacian）。DeltaConv 学会组合这些算子，并通过添加非线性项支持各向异性。

DeltaConv：学习各向异性算子

每个操作要么输出标量值特征，要么输出矢量值特征。我们连接每个流中属于它的所有特征，然后用参数化函数组合这些特征

\[v_i' = h_{\theta_0}(v_i, (GX)_i, (LV)_i)\] \[x_i' = h_{\theta_1}(x_i, (DV)'_i, (-DJV)'_i, ||v'_i||) + \max_{j \in \mathcal{N}_i} h_{\theta_2}(x_j). \quad (6)\]

我们使用撇号来表示 \(l+1\) 层的特征。所有其他特征来自于层 \(l\)。\(h_{\theta_1}\) 和 \(h_{\theta_2}\) 表示标准 MLPs。\(h_{\theta_0}\) 表示用于矢量的 MLP。矢量 MLP 能够缩放和求和矢量，公式（6）。

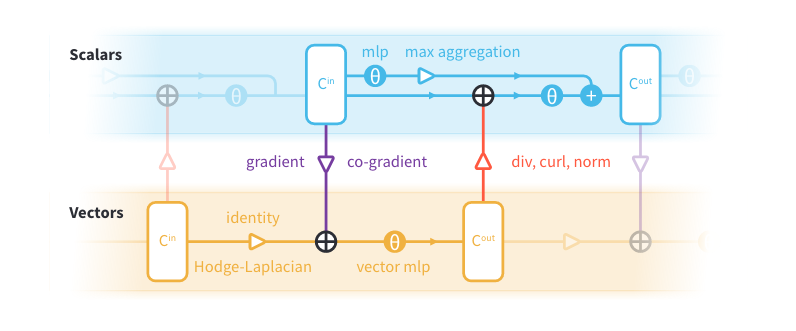
这意味着它们不对单独的向量系数工作，并且是坐标无关的。回想一下，\(V \in \mathbb{R}^{2N\times C^{(l)}}\)将每个点的向量系数交织在列中。向量MLP被应用到\(V\)上，如下所示：

\[V' = \sigma(VW)\quad (7)\]

其中 \(W \in \mathbb{R}^{C^{(l)}\times C^{(l+1)}}\)是一个权重矩阵，而 \(\sigma\)是一个非线性函数。矩阵乘法将 \(W\)与向量范数相结合，线性组合了向量特征，但向量的单个系数并没有混合。在向量MLP被应用之前，我们将输入特征的90度旋转向量连接起来。这使得MLP也能旋转向量特征，并且丰富了操作符集合。例如，90度旋转的梯度是共梯度。向量MLP可以学习结合来自局部邻域的信息（通过梯度和霍奇-拉普拉斯算子），以及来自不同通道的信息（通过恒等函数）。方程6的示意图可以在图4中找到。

虽然方程6以MLP和特征串联的形式表述了DeltaConv，另一种观点是将方程6中的操作视为线性组合基本操作符，并在它们之间用非线性函数进行组合，以形成各向异性的几何运算符。

DeltaConv 的属性

DeltaConv的构建模块，例如梯度、散度和旋度，以及它们与非线性的结合，使DeltaConv能够构建非线性各向异性卷积滤波器。这一点通过Perona-Malik滤波器在图2中的例子来说明。向量流还允许DeltaConv处理向量特征及其相对方向，直接使用相应的运算符。

DeltaConv的公式是以光滑的微分运算符为基础，不限于特定的表面表示。在这项工作中，我们为点云和图像实现了DeltaConv，然而，这些概念可以推广到其他表现形式。例如，对于网格，可以使用有限元离散化[Brandt et al. 2017]或离散外微积分[Crane et al. 2013a]来实现。

DeltaConv是坐标无关的，这意味着在DeltaConv中使用的权重并不依赖于切线基底的选择。例如，对同一形状的前向传递，如果基底的选择不同，仍然会导致相同的输出和权重更新。与坐标无关的原因在于，DeltaConv 中的所有基本操作，如应用几何算子和向量 MLP，都与坐标无关。据微分几何学所知，无论选择哪个基，都可以得到相同的几何运算结果[O’Neill 1983]。这个属性通过运算符的离散化得以保留，因此DeltaConv也继承了这一属性。

最后，DeltaConv的每一个构建模块都是等距不变的。这意味着如果一个形状发生了等距变形，DeltaConv是不会改变的。这个属性对于那些形状发生刚性或非刚性变形的任务是有益的。如果表面方向被翻转，切线平面中的旋转也会翻转。如果仅使用梯度和散度，DeltaConv对此具有鲁棒性。

实验

我们通过与最新技术在分类和分割上的比较来验证我们的方法。此外，我们进行消融研究，以便更深入地了解向量流对各向异性、准确性和效率的影响。

实施细节

在我们的实验中，我们使用基于DGCNN [Wang et al. 2019]的网络架构。我们用DeltaConv块替换了每个EdgeConv块（见图4），并且没有使用动态图组件。这些网络在局部邻域上单一尺度运作。尽管架构简单，DeltaConv仍然实现了最先进的结果。为了展示架构优化对DeltaConv的意义，我们还测试了在KPFCNN [Thomas et al. 2019]中使用的U-ResNet架构，但是将编码器中的卷积块用DeltaConv块替换。在下采样块中，我们通过平行运输池化向量特征[Wiersma et al. 2020]。更多细节在补充材料中提供。代码可在 deltaconv 上获取。

数据变换。对于每个形状，计算一个k-n图，用于标量流中的最大化聚合。当必要时，它被用来估算法线并构建梯度。在每项实验中，我们将xyz坐标作为输入来使用网络，并且使用随机尺度和平移，类似于先前工作的数据增强。一些数据集需要特定的增强，这些在它们各自的部分有详细说明。

训练。网络中的参数通过随机梯度下降（SGD）进行优化，初始学习率为0.1，动量为0.9，并设定了一个0.0001的终止学习率。参数使用余弦退火调度器[Loshchilov and Hutter 2017]更新，这会将学习率降低到0.001。

附录

A.离散化算子

梯度。我们通过[Liang 和 Zhao 2013]的方法构建一个离散梯度，使用移动最小二乘法。我们逐步演示了如何从黎曼几何的一般公式开始导出梯度，并在设置允许的情况下简化术语。

我们在局部拟合一个表面块来估计每个点 \(p\) 的度量，使用移动最小二乘法 [Nealen 2004]。表面块 \(\Gamma: \mathbb{R}^2 \rightarrow \mathbb{R}^3\)，通常称为蒙日(Monge)块，用二次多项式 \(h(u, v)\) 来描述点 \(p\) 处的切平面上的表面，其给出公式为：

\[\Gamma(u, v) = [u, v, h(u, v)]^T \quad (8)\]

其中，\(u, v\) 表示切平面中的局部坐标。由于表面块应该插值点 \(p\) 和表面法线，因此点 \(p\) 处的块的法线应该与切平面的法线一致，\(h(u, v)\) 的常数项和线性项消失。

\[h(u, v) = \alpha_1 u^2 + \alpha_2 uv + \alpha_3 v^2 \quad (9)\] \[h_u = 2\alpha_1 u + \alpha_2 v \quad (10)\] \[h_v = \alpha_2 u + 2\alpha_3 v \quad (11)\]

度量给出为：

\[g = \begin{bmatrix}1 + h_u^2 & h_uh_v \\h_uh_v & 1 + h_v^2\end{bmatrix} \quad (12)\]