Доп. главы по Мат. Анализу

Несколько полезных книг

• Лекции по математическому анализу
• Сборник задач и упражнений по математическому анализу
• 吉米多维奇数学分析习题集
• Математический анализ в задачах и упражнениях том 1
• Математический анализ в задачах и упражнениях том 3

Действительные числа

Опр. Непустое множество называется множеством действительных (вещественных) чисел, а его элементы — действительными (вещественными) числами, если на определены операции сложения и умножения и отношение порядка, удовлетворяющие следующим аксиома.

1. Аксиомы сложения \((a,b\to a+b)\):
   1. Коммутативность: \(a+b=b+a, \forall a,b\in \mathbb{R}\);
   2. Ассоциативность: \(a+(b+c)=(a+b)+c\);
   3. \(\exists 0\in \mathbb{R}:a+0=a,\forall a\in \mathbb{R}\);
   4. \(\forall a\in \mathbb{R},\exists (-a)\in \mathbb{R}:a+(-a)=0,(-a)\) называется противополжным числом для \(a\).

2. Аксиомы умножения \((a,b\to ab)\):

   1. Коммутативность: \(ab=ba, \forall a,b\in \mathbb{R}\);
   2. Ассоциативность: \(a(bc)=(ab)c\);
   3. \(\exists 1\in \mathbb{R}, 1\ne 0:a1=a,\forall a\in \mathbb{R}\);
   4. \(\forall a\in \mathbb{R},a\ne 0,\exists \frac{1}{a}\in \mathbb{R}:a\frac{1}{a}=1,\frac{1}{a}\) называется обратным числом для \(a\).

3. Связь сложения и умножения:

   1. \((a+b)c=ac+bc,\forall a,b,c\in \mathbb{R}\) - дистрибутивность умножения относительно сложения.

4. Аксиомы порядка (для любых \(a,b\in \mathbb{R}\) установлено отношение \(a\le b\) или \(a\ge b\)):

   1. \(a\le b,b\le a \Rightarrow a=b,\forall a,b\in \mathbb{R}\);
   2. \(a\le b,b\le c \Rightarrow a\le c,\forall a,b,c\in \mathbb{R}\).

5. Связь сложения и порядка:

   1. \(a\le b\Rightarrow a+c\le b+c,\forall a,b,c\in \mathbb{R}\).

6. Связь умножения и порядка:

   1. \(0\le a, 0\le b\Rightarrow 0\le ab,\forall a,b,c\in \mathbb{R}\).

7. Аксиома непрерывности (вариант принципа Дедекинда):

   1. Пусть \(A,B\) - непустые подмножества \(\mathbb{R}\), такие, что

      \[a\le b, \forall a\in A, \forall b\in B\]

      Тогда существует \(c\in \mathbb{R}\):

      \[a\le c\le b, \forall a\in A, \forall b\in B\]

实数集合就是满足以上性质的非空集合，其中的元素叫做实数。

1. 对于加法：满足交换律，结合率，有零元和逆元，
2. 对于乘法：满足交换律，结合率，有单位元和逆元，
3. 乘法对加法满足分配率，
4. 顺序公理以及连续性公理。

Теорема о точной грани

Теорема. (о существовании верхней (нижней) грани). Всякое непустое ограниченное сверху (снизу) числовое множество имеет верхнюю (нижнюю) грань.

该定理可以表述为：所有具备上界的非空数集都有上确界（下界和下确界同理）。

Доказательство. проведём лишь для верхней грани. Пусть \(A\) — непустое ограниченное сверху множество. Рассмотрим непустое множество \(B\), элементами которого являются все числа \(b\), ограничивающие множество \(A\) сверху.

Тогда

\[a\le b, \forall a\in A, \forall b\in B\]

В силу аксиомы непрерывности для некоторого \(c\in \mathbb{R}\):

\[a\le c\le b, \forall a\in A, \forall b\in B\]

Покажем, что \(\exists \sup A=c\). Первое условие из определения верхней грани выполняется для с в силу левого из неравенств.

Убедимся, что выполняется и второе. Пусть \(c'<c\). Тогда \(c'\in B\), так как для каждого элемента из \(В\) выполняется правое из неравенств. Следовательно, \(c'\) не ограничивает множество \(А\) сверху, т. е.

\[\exists x_{c'} \in A:x_{c'}>c'\]

так что второе условие также выполняется.

Следовательно, \(c=\sup A\) и теорема доказана.

该证明过程核心在于“实数系的完备公理”，戴德金完备性（вариант принципа Дедекинда）的表述是：如果实数集合被任意两个非空集合所分割，其中一个集合中的所有元素总是小于另一个集合中的任何元素，那么存在一个实数，它要么是第一个集合的最大元素，要么是第二个集合的最小元素。

Счетность множества рациональных чисел

Опр. Множество называется счётным,еслионо эквивалентно множеству натуральных чисел, иначе говоря, если его можно занумеровать всеми натуральными числами.

如果一个集合可以通过自然数来编号，那么这个集合就是可数的。

Теорема. Множество рациональных чисел счётно.

Доказательство. Составим таблицу чисел (открытую снизу и справа), содержащую все рациональные числа:

Будем двигаться по клеткам этой таблицы из левого верхнего угла по следующему пути:

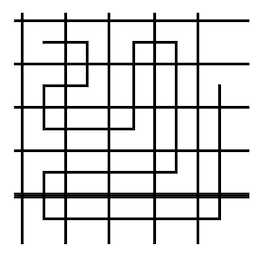
нумеруя встречающиеся в клетках рациональные числа и пропуская при этом те из них, которые ранее уже встречались.

Очевидно, таким способом мы занумеруем все рациональные числа всеми натуральными, что и требовалось доказать.

由之前可数的定义可以自然而然的将每一个有理数通过这个方法进行的编号，以此来证明有理数是可数的。

Несчетность множества действительных чисел

Теорема. (Кантора). Множество всех точек отрезка \([0,1]\) несчётно.

Доказательство. Допустим противное.

Тогда все точки отрезка \([0,1]\) можно занумеровать: \(x_1,x_2,x_3,\cdots\).

首先，利用反证法：假设\([0,1]\)上的点是可数的，即可以使用\(x_1,x_2,x_3,\cdots\)进行标号。

Поделим отрезок \([0,1]\) на три равных отрезка и обозначим через \([a_1,b_1]\) один из них, свободный от точки \(х_1\).

Поделим \([a_1,b_1]\) на три равных отрезка и обозначим через \([a_2,b_2]\) один из них, свободный от точки \(х_2\).

Продолжая процесс, получим систему вложенных отрезков \(\{[a_n,b_n]\}^{\infty }_{n=1}\). По теореме о вложенных отрезках существует точка \(с\), принадлежащая всем отрезкам системы. Эта точка \(с\) не совпадает ни \(с\) одной из занумерованных точек \(х_1,x_2,x_3\cdots\), так как любая из них \(x_j\) не содержится в отрезке \([a_j,b_j]\), в то время как \(с\) содержится в этом отрезке.

然后我们将当前区间三等分，一定能找到一个不包含点\(x_1\)的区间，

在这个区间里，我们再次等分，一定也能找到一个不包含点\(x_2\)的区间，

继续下去，我们就能在每次划分区间时，依次避开之前所有的标号点\(x_1,x_2,x_3,\cdots\)，

这也就意味着我们可以设置这么一个区间套，避开来所有的标号点。

Итак, при допущении, что все точки отрезка \([0,1]\) занумерованы, мы пришли к противоречию, найдя точку \(c\in [0,1]\), отличную от каждой из занумерованных. Это противоречие показывает, что наше допущение неверно. Теорема доказана.

根据区间套定理，这个区间套到极限时，一定是存在唯一一个点\(c\)在这个区间套里的，恰巧它又避开了之前所有的标号点，产生了矛盾，得证。